研究室に配属されたばかりの新入生や、これからRで統計分析を始めたいと思っている方へ向けて、【R講座】では、RとRStudioの基本的な使い方から統計手法の選び方、基本的なデータ分析方法を解説しています。特にRが初めての方でも安心して学べるように、RStudioのクリック操作も紹介していきます。実際のコード例を交えながら進めるので、これからの研究やデータ分析に、役立てていただけたら嬉しいです。

みなさん、こんにちは!
ここでは、この回で紹介したクラスカル・ウォリス検定について解説しています。
- クラスカル・ウォリス検定の概要
- クラスカル・ウォリス検定の方法
- 結果の見方
クラスカル・ウォリス検定とは

クラスカル・ウォリス検定は、3群以上の順位データを比較するためのノンパラメトリック検定です。この検定は、一元配置分散分析のノンパラメトリック版とも言えます。
クラスカル・ウォリス検定を実施する際には以下の条件を確認します。
- 対応の有無:独立した群
- 正規性:不要
- 等分散性:等分散を仮定
- 群数:2群以上
- データ尺度:順序尺度または比例尺度・間隔尺度
クラスカル・ウォリス検定では次の仮説を設定します。
- 帰無仮説(H0):全ての群の分布が同じである
- 対立仮説(H1):少なくとも1つの群の分布が他と異なる
関数の構造と引数オプション

Rでクラスカル・ウォリス検定を行うには、kruskal.test()
# ベクトルを使う方法
kruskal.test(x, g)
# フォーミュラを使う方法
kruskal.test(formula, data, subset, na.action, ...)
- x : 数値データのベクトル、または数値データのリスト
- g : x に対応するグループを示すベクトルまたは因子
- formula : 応答変数 ~ グループ の形でデータを指定する式
- data : formula を適用するデータフレームまたは行列
- subset : 使用するデータの一部を指定するためのオプション
- na.action : 欠損値 (NA) をどのように扱うかを指定する関数
- ... : その他の引数
分析の実践

次のステップでデータを分析していきます。
- STEP 1データの読み込み
csvファイルからデータを読み込みます。
- STEP 2データの型変換(キャスト)
読み込んだデータの要因データを、Factor型に変更します。
- STEP 3クラスカル・ウォリス検定の実行
kruskal.test - STEP 4結果の出力
計算された結果がコンソールペインに出力されます。
使用するデータ

この講座では、説明のために同じ CSV データを使い回しています。
実際には、データの性質(分布・尺度・サンプル数など)に合わせて、適切な統計検定を選びましょう。
このcsvファイルには次のデータが含まれています。
| Temperature (°C) | Height (cm) | Weight (g) |
|---|---|---|
| 25 | 11.408563356834 | 34.032819857028 |
| 25 | 9.45823963789889 | 54.9096737259706 |
| 25 | 10.2786647241064 | 54.2160336538475 |
| 25 | 9.8060272553297 | 68.739038985953 |
| 25 | 11.5761581812187 | 60.3451432394433 |
| 25 | 8.52445236473948 | 50.8181031035401 |
| 25 | 9.85539179268946 | 49.1747623798284 |
| 25 | 8.92498980918183 | 56.060734308621 |
| 25 | 10.4065427319449 | 41.125798546829 |
| 25 | 12.2292622016409 | 51.0542139019377 |
| 30 | 13.4855029917497 | 103.528744733185 |
| 30 | 14.938292577988 | 105.503933584551 |
| 30 | 14.852729209961 | 88.6566903148316 |
| 30 | 16.541593068827 | 114.623515387464 |
| 30 | 14.0181443311961 | 107.021167106676 |
| 30 | 15.4965781726617 | 125.071111484834 |
| 30 | 16.6969478807231 | 81.0997285637598 |
| 30 | 14.7392636914319 | 94.1018720980883 |
| 30 | 14.2940714143323 | 82.8549770315418 |
| 30 | 14.8388214938277 | 95.790021021833 |
| 35 | 15.5013218277237 | 78.1014137650469 |
| 35 | 13.9864603295052 | 92.025705860145 |
| 35 | 16.6147522354681 | 70.5661519563607 |
| 35 | 15.0056419848525 | 63.0140291668191 |
| 35 | 12.0951009396544 | 71.926190857745 |
| 35 | 13.8928351810313 | 81.2105420273818 |
| 35 | 16.5475669326183 | 76.8190219140427 |
| 35 | 14.0231696496533 | 88.1840093119247 |
| 35 | 14.8984965523683 | 72.0109068656934 |
| 35 | 15.0426502497967 | 58.5177825784117 |
データの読み込み
まずは、次のコードを使って、オブジェクト「data」にread.csv()関数でcsvファイルのデータを代入します。
# データの読み込み
data <- read.csv(file.choose(),
check.names = F)データの前処理
次に、データの因子変換をします。
Rでは説明変数をFactor型のデータとします。今回の分析ではTemperature (°C)を説明変数とするので、as.factor()関数でデータ型をinteger型からFactor型に変更します。
# 説明変数をデータ型をFactor型に変更
data$`Temperature (°C)` <- as.factor(data$`Temperature (°C)`)実行結果は、Environmentタブで確認できます。Temperature (°C)のデータ型がinteger型(左図)からFactor型(右図)に変わります。
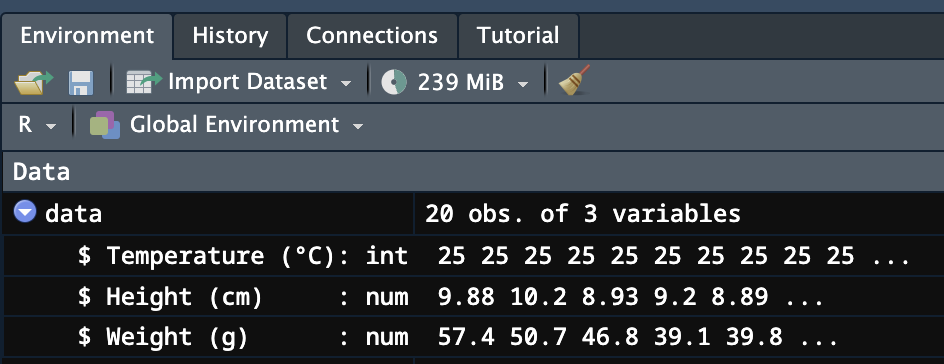
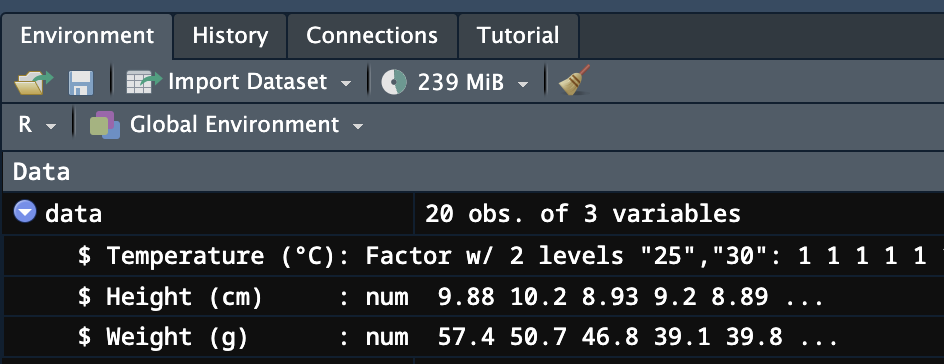
バッククォート「`」について、少しだけ補足します。
R言語においてバッククォート「 ` 」で文字列を挟むと、通常は予約語や空白、特殊文字を含む名前を使うことができます。これにより、通常は無効な識別子として扱われる文字列を有効なオブジェクト名として扱うことができます。
ヘッダー名であるHeight (cm)は、スペース「 」や括弧「()」が含まれているため、そのままオブジェクト名として使用できませんが、バッククォートを使うことでオブジェクト名として使用できます。
クラスカル・ウォリス検定
入力法方はフォーミュラ型で、目的変数はHeight (cm)のデータ、説明変数はTemperature (°C)としています。目的変数を変更すれば、Weight (g)のデータを検定できます。
# クラスカル・ウォリス検定の実行
kruskal.test(data$`Height (cm)` ~ data$`Temperature (°C)`)結果の見方
検定を実行した結果は、コンソールペインに表示されます。
Kruskal-Wallis rank sum test
data: data$`Height (cm)` by data$`Temperature (°C)`
Kruskal-Wallis chi-squared = 18.97, df = 2, p-value = 7.597e-05この結果から、p値が0.05より小さいため、少なくとも1つのグループの中央値に有意な差があると判断することができます。
| 項目 | 説明 |
|---|---|
有意水準 (α) | 帰無仮説を棄却する基準。通常 0.05(5%) や 0.01(1%) を使用する。 例: α = 0.05なら、5%未満の確率で偶然起こる差を「有意」と判断する。 |
| p値 | 検定統計量が観測された値以上になる確率。 p値 < 有意水準 (α) なら、統計的に有意と判断し、帰無仮説を棄却する。 |
| 統計的に有意とは? | 「偶然の変動では説明できない差がある」と判断すること。ただし「実験的に重要」や「因果関係がある」とは限らない。 |
| 信頼区間 (Confidence Interval, CI) | 母集団の真の値(2つのグループの平均値の差)が含まれる範囲を示す。例えば 95%信頼区間 は、繰り返し実験したときに95%の確率で真の値(平均値の差)を含む。 |
| 信頼区間と有意性の関係 | もし信頼区間が ゼロ(または比較対象の値)を含まなければ、統計的に有意と判断できる。 例:平均差の95%信頼区間が (0.5, 2.3) なら、有意水準5%で有意。 |
| 注意点 | 統計的有意でも「効果の大きさ(実用的な意味)」とは異なる。 p値が大きくても「差がない」とは言えない(サンプル数が少ない可能性)。 |
まとめ
- クラスカル・ウォリス検定の概要
- ノンパラメトリック・等分散・3群以上
- 間隔・比例・順序尺度
- クラスカル・ウォリス検定の方法
- ベクトル型の場合:
kruskal.test(ベクトル1,ベクトル2) - フォーミュラ型の場合:
kruskal.test(目的変数 ~ 説明変数)
- ベクトル型の場合:
- 結果の見方
- 有意水準・p値・信頼区間から判断
- 統計的な意味と実用的な意味に注意

ここでは、Rを使用してクラスカル・ウォリス検定を行う方法について解説しました。
配布したcsvデータにはWeight (g)のデータもあるので、コードを書き換えて練習してみてください。
Rでは、コードの文法が正しければどんな統計手法でも計算が実行されてしまうため、結果が出たからといって安心するのは危険です。統計解析では、データの種類や前提条件に適した手法を選ぶことが重要であり、誤った検定を適用すると意味のない結果を得てしまう可能性があります。
そのため、単にコードを動かすだけでなく、
- データの分布(正規分布かどうか)
- 変数の尺度(カテゴリーデータか、連続データか)
- サンプルサイズ(母数が少ないと適さない検定もある)
などを考慮し、統計の知識をもとに適切な解析方法を選択する必要があります。

最後に、実際に私が購入したおすすめできる本を厳選して紹介します。
アフィリエイトリンクを使っていますが、クリックしていただけると更新の励みになります。よろしければぜひご覧ください!

Rによる統計解析 単行本 – 2009/4/1

実際のコードや技法が詰め込まれたわかりやすい書籍です。
Rで統計解析をするときの辞書的な本として愛用しています。

実験で使うとこだけ生物統計1 キホンのキ 決定版 単行本 – 2024/7/25

統計解析の基礎をわかりやすく解説している本です。
難しい用語や数式が少ないので、統計初心者におすすめです。

実験で使うとこだけ生物統計2 キホンのホン 決定版 単行本 – 2024/7/25

キホンのキに続き、統計検定の本質から検定法を説明している書籍です。
実験計画を立てる前におすすめしたい一冊です。



